osculateur

osculateur

osculateur, trice [ ɔskylatɶr, tris ] adj.
• 1701; du lat. osculari « embrasser »
♦ Géom. Se dit d'une courbe, d'une surface, etc., qui, en un point donné, a le contact de l'ordre le plus élevé avec une autre courbe, surface. Plan osculateur; surface osculatrice.

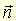● osculateur, osculatrice adjectif (latin osculari, baiser) Cercle osculateur à une courbe en un point M, cercle centré sur le centre de courbure C de la courbe en M, et de rayon CM. Plan osculateur à une courbe gauche en un point M, plan défini par M et les vecteurs et du trièdre de Frénet en ce point. ● osculateur, osculatrice (expressions) adjectif (latin osculari, baiser) Cercle osculateur à une courbe en un point M, cercle centré sur le centre de courbure C de la courbe en M, et de rayon CM. 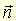Plan osculateur à une courbe gauche en un point M, plan défini par M et les vecteurs et du trièdre de Frénet en ce point.

⇒OSCULATEUR, -TRICE, adj.
GÉOM. [En parlant d'une courbe, d'une surface] Qui a un contact d'ordre maximal avec une autre courbe ou une autre surface en un point donné. Surface osculatrice. [Leibniz] traite de la courbure des courbes, et du cercle osculateur, pour aboutir en 1692 (...) aux principes généraux sur le contact des courbes planes (BOURBAKI, Hist. math., 1960, p.212). Cercle osculateur en un point M d'un arc géométrique (BOUVIER-GEORGE Math. 1979).
♦Plan osculateur. ,,Plan le plus proche possible d'un élément non plan d'une courbe`` (Sc. 1962). Quand elle [la courbe] est plane, le plan osculateur n'est plus autre chose que le plan même de la courbe (POISSON, Mécan., t.1, 1811, p.371).
Prononc. et Orth.:[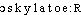], fém. [-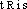]. Att. ds Ac. 1935. Étymol. et Hist. 1752 géom. (DE COURTIVRON, Traité d'optique, p.88 ds DG). Formé sur le rad. lat. de osculation (rad. du part. passé de osculare et osculari «baiser»); suff. -eur2.

osculateur, trice [ɔskylatœʀ, tʀis] adj.
ÉTYM. 1752; du lat. osculari « embrasser », de os, oris « bouche ».
❖
♦ Géom. Se dit d'une courbe qui, en un point donné, a le contact de l'ordre le plus élevé avec une autre courbe.
♦ Par anal. || Plan osculateur; surface osculatrice.

Encyclopédie Universelle. 2012.

Игры ⚽ Нужно решить контрольную?

Regardez d'autres dictionnaires:

  • osculateur — osculateur, trice (o sku la teur, tri s ) adj. Terme de géométrie. Cercle osculateur, courbe osculatrice, solide osculateur, cercle, courbe, solide qui a deux éléments infinitésimaux communs avec une autre courbe, présente la même courbure qu… …   Dictionnaire de la Langue Française d'Émile Littré

  • OSCULATEUR, TRICE — adj. T. de Géométrie Il se dit d’une Courbe, d’une surface d’une nature déterminée, qui a le contact d’ordre le plus élevé possible en un point d’une courbe donnée, d’une surface donnée. Cercle osculateur, sphère osculatrice …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • Cercle osculateur — Au point M de la courbe rouge, le cercle osculateur (en pointillés) approche mieux la courbe qu un cercle tangent quelconque (passant par N). Son centre O et son rayon R sont le centre de courbure et le rayon de courbure de la courbe en M …   Wikipédia en Français

  • Cercle Osculateur — Tangente et cercle de courbure en un point P de la courbe C En géométrie différentielle, le cercle osculateur ou cercle de courbure est un outil permettant la description locale des courbes. Il s agit d un cercle qui approche la courbe mieux que… …   Wikipédia en Français

  • Cercle osculateur à une courbe en un point M — ● Cercle osculateur à une courbe en un point M cercle centré sur le centre de courbure C de la courbe en M, et de rayon CM …   Encyclopédie Universelle

  • Plan osculateur à une courbe gauche en un point M — ● Plan osculateur à une courbe gauche en un point M plan défini par M et les vecteurs et du trièdre de Frénet en ce point …   Encyclopédie Universelle

  • osculatrice — ● osculateur, osculatrice adjectif (latin osculari, baiser) Cercle osculateur à une courbe en un point M, cercle centré sur le centre de courbure C de la courbe en M, et de rayon CM. Plan osculateur à une courbe gauche en un point M, plan défini… …   Encyclopédie Universelle

  • Cercle De Courbure — Cercle osculateur Tangente et cercle de courbure en un point P de la courbe C En géométrie différentielle, le cercle osculateur ou cercle de courbure est un outil permettant la description locale des courbes. Il s agit d un cercle qui approche la …   Wikipédia en Français

  • Cercle de courbure — Cercle osculateur Tangente et cercle de courbure en un point P de la courbe C En géométrie différentielle, le cercle osculateur ou cercle de courbure est un outil permettant la description locale des courbes. Il s agit d un cercle qui approche la …   Wikipédia en Français

  • Courbe — En géométrie, le mot courbe, ou ligne courbe désigne certains sous ensembles du plan, de l espace usuels. Par exemple, les droites, les segments, les lignes polygonales et les cercles sont des courbes. La notion générale de courbe se décline en… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”